在测试过程中,会遇到多个因素决定输出结果的情况。
比如在线商城消费满返送券,需要根据活动有效期,券的有效期,券的数量,用户消费金额满足送券金额的梯度来最终决定给用户送券的数量或金额。假设活动有效期,券的有效期,券的数量,用户消费金额都有三种状态值,这样的场景我们该怎么设计测试用例?
-----------------------------------思考的分割线美美的来一条-----------------------------------
让我们早早地引出本文的主题:测试用例设计之正交实验法

在科研和生产实践中,人们往往要做许多次实验来进行某项研究。实验结果一般由很多因素共同影响,因素的值不同产生不一样的试验结果。如果想把每个因素的每个值都要验证一遍,总验证次数就等于各因素的值的个数的乘积,而这个数往往超乎想象的巨大。
全面试验,即全组合,也叫笛卡尔积,是对每个因素的每个水平互相搭配进行试验/验证。
假设,我们要完成某一款车的燃油消耗试验,经分析主要由车辆速度、车辆重量、车辆窗户开闭状态三个因素影响(因素数=3),并且每个因素都有3种状态,分别为高中低(水平数=3)。那么要进行全面试验的话,我们需要完成 3 x 3 x 3 = 27 次的试验。
为了减少实验次数,我们必须选出那些最有代表性的例子来完成尽可能多的覆盖验证。
正交实验设计方法 依据Galois理论,从大量的(实验)数据(测试例)中挑选适量的、有代表性的点(例),从而合理地安排实验(测试)的一种科学实验设计方法。类似的方法有:聚类分析方法、因子方法方法等。
PS:Galois理论,即伽罗瓦理论,是用群论的方法来研究代数方程的解的理论,如果感兴趣自行度娘一下。
同样,我们需要对汽车的燃油消耗进行试验,通过正交设计计算(后面介绍计算方法),我们可以得出只要 9 次就可以完成试验,工作效率提升2倍。
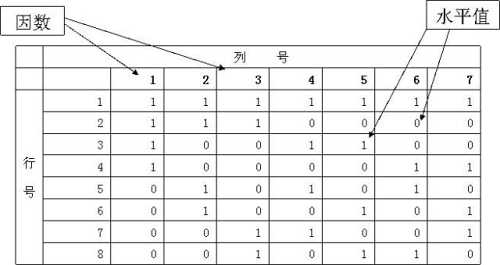
正交表是如何构成的?
行数(Runs):正交表中的行的个数,即试验的次数,也是我们通过正交实验法设计的测试用例的个数(这个根据常用正交表,进行套用。至于常用正交表,依然度娘;也可以在微信公众号(ceshibuluo)中输入 正交表 获取)。
因素数(Factors) :正交表中列的个数,即我们要测试的功能点。
水平数(Levels):任何单个因素能够取得的值的最大个数。正交表中的包含的值为从0到数“水平数-1”或从1到“水平数”。即要测试功能点的输入条件。
正交表的形式:
L行数(水平数^因素数),如L8(2^7)
用正交表设计测试用例的步骤
①有哪些因素(变量)。
②每个因素有哪几个水平(变量的取值)
如何确定每个因素的水平?
根据因素的取值范围或集合,采用等价类划分、边界值分析以及其他软件测试技术,在每个因素的取值范围或集合内挑选出有效等价类、无效等价类、正好等于、刚刚大于或刚刚小于边界值等有代表性的测试值。
③选择一个合适的正交表。
如何在常用正交表中选择一个?
- 考虑因素(变量)的个数
- 考虑因素水平(变量的取值)的个数
- 考虑正交表的行数
- 取行数最少的一个
④把变量的值映射到表中。
⑤把每一行的各因素水平的组合做为一个测试用例。
⑥加上你认为可疑且没有在表中出现的组合。
举个栗子:因素数与水平数刚好符合正交表
第一步,确定因素及因素的水平